How to Solve the Difference Quotient

Steps to Solve

The difference quotient is an important part of mathematics, especially calculus. Given a function f(x), and two input values, x and x + h (where h is the distance between x and x + h), the difference quotient is the quotient of the difference of the function values, f(x + h) – f(x), and the difference of the input values, (x + h) – x.

Continuing on, we can simplify the denominator of this because the x cancels out, which you can see play out here.

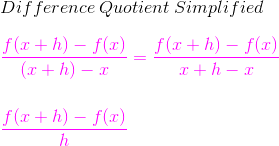We see that the difference quotient is as follows:

(f(x + h) – f(x)) / h

Great! We’ve got a formula for the difference quotient. Now, let’s consider the steps involved in solving this difference quotient. Any time we are given a formula, solving the formula is just a matter of finding the values of the variables and expressions involved in the formula, plugging them into the formula, and then simplifying. Therefore, the following steps are used to solve the difference quotient for a function, f(x).

1. Plug x + h into the function f and simplify to find f(x + h).
2. Now that you have f(x + h), find f(x + h) – f(x) by plugging in f(x + h) and f(x) and simplifying.
3. Plug your result from step 2 in for the numerator in the difference quotient and simplify.

Okay, three steps. We can handle this! Let’s try an example. Suppose we want to find the difference quotient for the function

g(x) = x2 + 3

As you can see here, we start by plugging the expression x + h into g, and simplifying.

As we can see, we get that g(x + h) = x2 + 2xh + h2 + 3. Next, we plug g(x + h) and g(x) into g(x + h) – g(x) and simplify.

As you can see, we end up with 2xh + h2. So far, so good! All we have left to do is plug this in for the numerator in the difference quotient and simplify.

We see that given the function g(x) = x2 + 3 and two input values of x and x + h, the difference quotient is 2x + h, where h is the difference between the two input values. That’s not so bad!

Geometrical Interpretation

Okay, we know the formula for the difference quotient and we know how to solve the difference quotient, but why is this useful? To understand this, let’s consider the geometrical interpretation of the difference quotient.

When we introduced the formula for the difference quotient,

(f(x + h) – f(x)) / h

we defined it in terms of a given function f(x), and two input values x and x + h. Let’s think about that for a second. If we have input values of x and x + h, then the corresponding function values, or y-values, are f(x) and f(x + h), so we’re considering two points on the function; (x, f(x)) and (x + h, f(x + h)).

Now, notice that before we simplified the difference quotient, it was the difference of the function values (or y-values) f(x + h) and f(x) divided by the difference in the x-values, x + h and x.

(f(x + h) – f(x)) / (x + h) – x